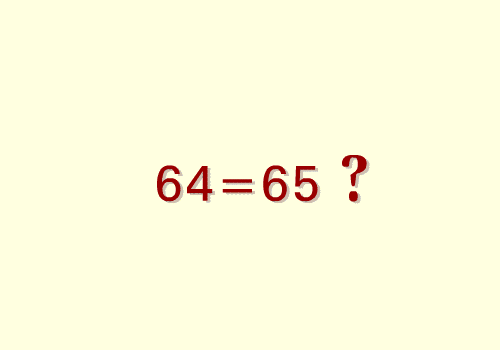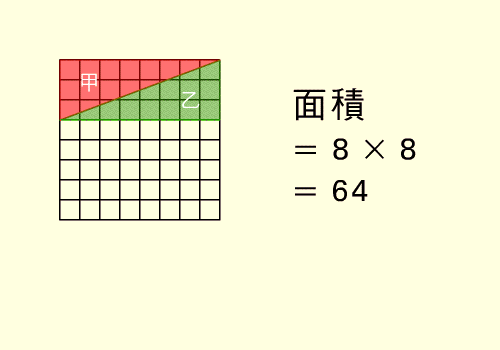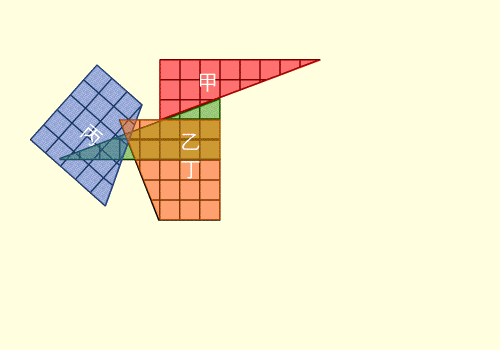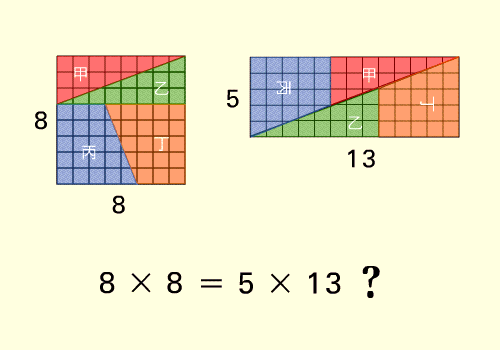- Esercitatore: Dr. Carmelo Finocchiaro
Studio N. 201
Ricevimento Studenti: lunedì dalle ore 17.10 alle ore 19.10
carmelo(at)mat.uniroma3.it
__________________________________
II Settimana (29 Settembre - 3 Ottobre)
Esercizi su tavole di verità, equivalenza logiche e tautologie. Esercizi di teoria degli insiemi. Applicazioni della forma standard del Principio di Induzione. Calcolo del numero di sottoinsiemi di un insieme con $n$ elementi.
 Esercizi per casa 1.
Esercizi per casa 1.
__________________________________
 10 Ottobre 2014
10 Ottobre 2014
 15 Ottobre 2014
15 Ottobre 2014
 24 Ottobre 2014
24 Ottobre 2014
 29 Ottobre 2014
29 Ottobre 2014
 31 Ottobre 2014
31 Ottobre 2014
 14 Novembre 2014
14 Novembre 2014
 21 Novembre 2014
21 Novembre 2014
 28 Novembre 2014
28 Novembre 2014
 4 Dicembre 2014
4 Dicembre 2014
 12 Dicembre 2014
12 Dicembre 2014
 19 Dicembre 2014
19 Dicembre 2014
 9 Gennaio 2015
9 Gennaio 2015
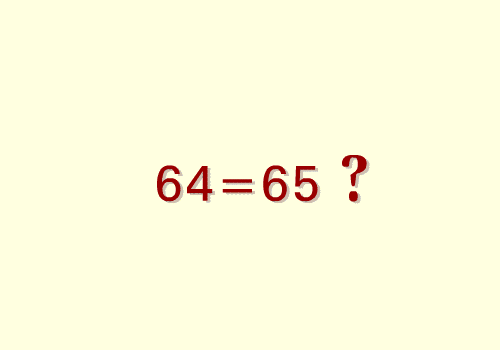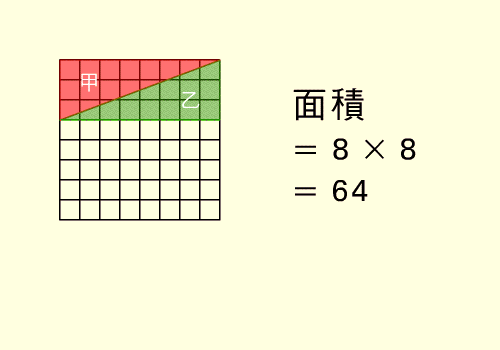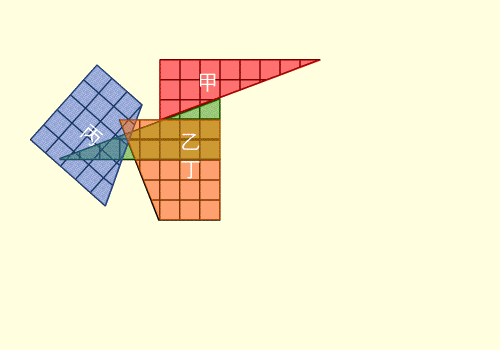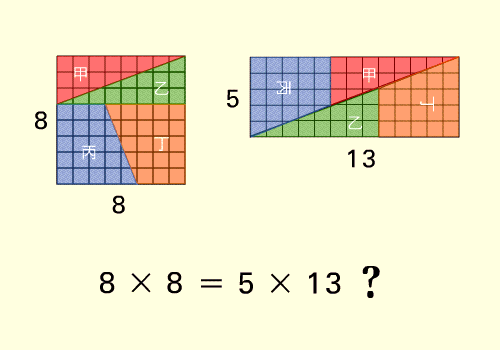
Esercizi su tavole di verità, equivalenza logiche e tautologie. Esercizi di teoria degli insiemi. Applicazioni della forma standard del Principio di Induzione. Calcolo del numero di sottoinsiemi di un insieme con $n$ elementi.
 Esercizi per casa 1.
Esercizi per casa 1.
__________________________________
III Settimana (6 Ottobre - 10 Ottobre)
Il principio di "ampia" induzione e suo uso. Ogni numero intero positivo è somma di una collezione finita di numeri di Fibonacci a due a due non consecutivi. Calcolo di MCD e di identità di Bezout ad essi relative. Equazioni diofantee lineari in due incognite. Dati numeri interi $a,b,c$, l'equazione diofantea $aX+bY=c$ ammette soluzioni se, e soltanto se, il MCD$(a,b)$ divide $c$. Uso dell'Algoritmo di Euclide per determinare una soluzione di una fissata equazione diofantea compatibile. Data una soluzione $(x_0,y_0)\in \mathbf Z\times \mathbf Z$ dell'equazione diofantea $(\star)$ $aX+bY=c$, con MCD$(a,b)=1$, tutte e sole le soluzioni di $(\star)$ sono del tipo $(x_0+bt,y_0-at)$, al variare di $t\in\mathbf Z$. Esempi. Svolgimento di alcuni esercizi assegnati per casa.
Il principio di "ampia" induzione e suo uso. Ogni numero intero positivo è somma di una collezione finita di numeri di Fibonacci a due a due non consecutivi. Calcolo di MCD e di identità di Bezout ad essi relative. Equazioni diofantee lineari in due incognite. Dati numeri interi $a,b,c$, l'equazione diofantea $aX+bY=c$ ammette soluzioni se, e soltanto se, il MCD$(a,b)$ divide $c$. Uso dell'Algoritmo di Euclide per determinare una soluzione di una fissata equazione diofantea compatibile. Data una soluzione $(x_0,y_0)\in \mathbf Z\times \mathbf Z$ dell'equazione diofantea $(\star)$ $aX+bY=c$, con MCD$(a,b)=1$, tutte e sole le soluzioni di $(\star)$ sono del tipo $(x_0+bt,y_0-at)$, al variare di $t\in\mathbf Z$. Esempi. Svolgimento di alcuni esercizi assegnati per casa.
__________________________________
IV Settimana (13 Ottobre - 17 Ottobre)
Esercizi di ricapitolazione su aritmetica, numeri primi, teoria degli insiemi (filtri e insiemi transitivi). Ordini parziali su un insieme. L'ordine canonico $\mathbf R$ (e $\mathbf N$). L'ordine di divisibilità su $\mathbf N^+$. L'ordine dell'inclusione sulla famiglia delle parti di un insieme. L'ordine lessicografico. Il grafico di un ordine parziale, esempi.
 Esercizi per casa 2.
Esercizi per casa 2.
Esercizi di ricapitolazione su aritmetica, numeri primi, teoria degli insiemi (filtri e insiemi transitivi). Ordini parziali su un insieme. L'ordine canonico $\mathbf R$ (e $\mathbf N$). L'ordine di divisibilità su $\mathbf N^+$. L'ordine dell'inclusione sulla famiglia delle parti di un insieme. L'ordine lessicografico. Il grafico di un ordine parziale, esempi.
 Esercizi per casa 2.
Esercizi per casa 2.
__________________________________
V Settimana (20 Ottobre - 24 Ottobre)
Elementi massimali e minimali, massimo e minimo in insiemi parzialmente ordinati. Estremo inferiore e superiore di sottoinsiemi di insiemi parzialmente ordinati. Esempi ed esercizi vari. Calcolo della forma polare di un numero complesso. Esempi di relazioni di equivalenza e quozienti.
Radici $n$-esime di un numero complesso. Radici $n$-esime dell'unità e loro rappresentazione sulla circonferenza unitaria $\mathbf S^1$. Calcolo di inversi aritmetici. Equazioni lineari in una incognita a coefficienti in $\mathbf Z/n\mathbf Z$. L'equazione $[a]_nX=[b]_n$ ammette soluzioni se, e soltanto se $d:=$MCD$(a,n)$ divide $b$. Legame fra equazioni congruenziali ed equazioni diofantee. Calcolo del numero di soluzioni dell'equazione $[a]_nX=[b]_n$ (quando essa è compatibile). Applicazioni del piccolo Teorema di Fermat. Per ogni $a,b\in\mathbf Z$ e per ogni numero primo $p$, $(a+b)^p\equiv a^p+b^p$ (mod $p$). Se $p,q$ sono numeri primi distinti e $a\in\mathbf Z$ è tale che $a^p\equiv a$ (mod $q$) e $a^q\equiv a$ (mod $p$), allora $a^{pq}\equiv a$ (mod $pq$). Risoluzione per sostituzione di sistemi di equazioni congruenziali.
Elementi massimali e minimali, massimo e minimo in insiemi parzialmente ordinati. Estremo inferiore e superiore di sottoinsiemi di insiemi parzialmente ordinati. Esempi ed esercizi vari. Calcolo della forma polare di un numero complesso. Esempi di relazioni di equivalenza e quozienti.
__________________________________
VI Settimana (27 Ottobre - 31 Ottobre)
Radici $n$-esime di un numero complesso. Radici $n$-esime dell'unità e loro rappresentazione sulla circonferenza unitaria $\mathbf S^1$. Calcolo di inversi aritmetici. Equazioni lineari in una incognita a coefficienti in $\mathbf Z/n\mathbf Z$. L'equazione $[a]_nX=[b]_n$ ammette soluzioni se, e soltanto se $d:=$MCD$(a,n)$ divide $b$. Legame fra equazioni congruenziali ed equazioni diofantee. Calcolo del numero di soluzioni dell'equazione $[a]_nX=[b]_n$ (quando essa è compatibile). Applicazioni del piccolo Teorema di Fermat. Per ogni $a,b\in\mathbf Z$ e per ogni numero primo $p$, $(a+b)^p\equiv a^p+b^p$ (mod $p$). Se $p,q$ sono numeri primi distinti e $a\in\mathbf Z$ è tale che $a^p\equiv a$ (mod $q$) e $a^q\equiv a$ (mod $p$), allora $a^{pq}\equiv a$ (mod $pq$). Risoluzione per sostituzione di sistemi di equazioni congruenziali.
__________________________________
VII Settimana (10 Novembre - 14 Novembre)
Commenti sul alcuni degli esercizi della prima prova in itinere. Sia $\varphi$ l'indicatore di Eulero. Se $p$ è un numero primo e $h$ è un intero positivo, allora $\varphi(p^h)=p^h-p^{h-1}$. Procedura per il calcolo dell'indicatore di Eulero di ogni numero naturale. Uso del Teorema cinese dei resti per il calcolo delle soluzioni di un sistema di equazioni congruenziali. Metodo di sostituzione. Applicazioni del Teorema di Eulero. Calcolo delle ultime due cifre decimali di $7^{2002}$. Per ogni intero $n$ dispari non divisibile pr 5, il numero $n^4-1$ è divisibile per 80. Se $p,q$ sono primi distinti, allora $p^{q-1}+q^{p-1} \equiv 1$ (mod $pq$). Studio di iniettività e surgettività di funzioni.
 Esercizi per casa 3.
Esercizi per casa 3.
Un ricordo di Alexander Grothendieck (28 Marzo 1928 - 13 Novembre 2014)
Commenti sul alcuni degli esercizi della prima prova in itinere. Sia $\varphi$ l'indicatore di Eulero. Se $p$ è un numero primo e $h$ è un intero positivo, allora $\varphi(p^h)=p^h-p^{h-1}$. Procedura per il calcolo dell'indicatore di Eulero di ogni numero naturale. Uso del Teorema cinese dei resti per il calcolo delle soluzioni di un sistema di equazioni congruenziali. Metodo di sostituzione. Applicazioni del Teorema di Eulero. Calcolo delle ultime due cifre decimali di $7^{2002}$. Per ogni intero $n$ dispari non divisibile pr 5, il numero $n^4-1$ è divisibile per 80. Se $p,q$ sono primi distinti, allora $p^{q-1}+q^{p-1} \equiv 1$ (mod $pq$). Studio di iniettività e surgettività di funzioni.
 Esercizi per casa 3.
Esercizi per casa 3.Un ricordo di Alexander Grothendieck (28 Marzo 1928 - 13 Novembre 2014)
Raccolta di articoli su Grothendieck apparsi negli ultimi giorni.
__________________________________
VIII Settimana (17 Novembre - 21 Novembre)
Dati un insieme finito $X$ con $n$ elementi e una bigezione $f:X\longrightarrow Y$, allora $Y$ è finito e ha $n$ elementi. Se $X$ è finito e $Y\subsetneq X$, allora non esiste alcuna bigezione $X\longrightarrow Y$. Se invece $X$ è un insieme infinito, allora esistono un sottoinsieme proprio $Y$ di $X$ e una bigezione $X\longrightarrow Y$. Insiemi numerabili. Gli insiemi $\mathbf Z$ e $\mathbf N\times \mathbf N$ sono numerabili. Primo procedimento diagonale di Cantor. Ricerca di una bigezione esplicita $\mathbf N\times \mathbf N\longrightarrow \mathbf N$. Si identifichi la retta reale $\mathbf R$ con l'asse delle ascisse del piano e si consideri il punto $N(0,1)$ di $\mathbf S^1$: allora esiste una bigezione naturale $\mathbf S^1-\{N\}\longrightarrow \mathbf R$ (via proiezione stereografica). Generalizzazione in dimensione maggiore di 2. Svariate applicazioni del teorema fondamentale di spezzamento di una funzione. Dati due interi $r,s$ coprimi, esiste una bigezione naturale $\mathbf Z/rs\mathbf Z\longrightarrow (\mathbf Z/r\mathbf Z)\times (\mathbf Z/s\mathbf Z)$.
Dati un insieme finito $X$ con $n$ elementi e una bigezione $f:X\longrightarrow Y$, allora $Y$ è finito e ha $n$ elementi. Se $X$ è finito e $Y\subsetneq X$, allora non esiste alcuna bigezione $X\longrightarrow Y$. Se invece $X$ è un insieme infinito, allora esistono un sottoinsieme proprio $Y$ di $X$ e una bigezione $X\longrightarrow Y$. Insiemi numerabili. Gli insiemi $\mathbf Z$ e $\mathbf N\times \mathbf N$ sono numerabili. Primo procedimento diagonale di Cantor. Ricerca di una bigezione esplicita $\mathbf N\times \mathbf N\longrightarrow \mathbf N$. Si identifichi la retta reale $\mathbf R$ con l'asse delle ascisse del piano e si consideri il punto $N(0,1)$ di $\mathbf S^1$: allora esiste una bigezione naturale $\mathbf S^1-\{N\}\longrightarrow \mathbf R$ (via proiezione stereografica). Generalizzazione in dimensione maggiore di 2. Svariate applicazioni del teorema fondamentale di spezzamento di una funzione. Dati due interi $r,s$ coprimi, esiste una bigezione naturale $\mathbf Z/rs\mathbf Z\longrightarrow (\mathbf Z/r\mathbf Z)\times (\mathbf Z/s\mathbf Z)$.
__________________________________
IX Settimana (24 Novembre - 28 Novembre)
Per ogni intero positivo $n$, si denoti con $\mathcal U(\mathbf Z/n\mathbf Z)$ l'insieme degli invertibili di $\mathbf Z/n\mathbf Z$. Allora, dati interi coprimi $r,s$, la bigezione canonica $\mathbf Z/rs\mathbf Z\longrightarrow (\mathbf Z/r\mathbf Z)\times (\mathbf Z/s\mathbf Z)$ induce, per restrizione, una bigezione $\mathcal U(\mathbf Z/rs\mathbf Z)\longrightarrow \mathcal U(\mathbf Z/r\mathbf Z)\times \mathcal U (\mathbf Z/s\mathbf Z)$. Dunque, l'indicatore di Eulero $\varphi$ è moltiplicativo (i.e., per ogni $r,s\in\mathbf Z$ coprimi, si ha $\varphi(rs)=\varphi (r)\varphi(s)$). Una bigezione naturale fra un quoziente di $\mathbf R$ e $\mathbf S^1$. Caratterizzazione per l'irriducibilità di un polinomio di grado 2 o 3 in $A[T]$, dove $A\in\{\mathbf Q,\mathbf R,\mathbf C,\mathbf Z/p\mathbf Z, p\mbox{ primo}\}$. I polinomi irriducibili in $\mathbf C[T]$ sono precisamente quelli di grado 1. Se $z$ è radice complessa non reale di un polinomio $f\in\mathbf R[T]$, allora anche $\overline z$ è radice di $f$. Gli unici polinomi irriducibili di $\mathbf R[T]$ sono i polinomi di grado 1 e quelli di grado 2 che non hanno radici reali. Criterio di Eisenstein e sua versione reciproca. Esempi di fattorizzazione.
Per ogni intero positivo $n$, si denoti con $\mathcal U(\mathbf Z/n\mathbf Z)$ l'insieme degli invertibili di $\mathbf Z/n\mathbf Z$. Allora, dati interi coprimi $r,s$, la bigezione canonica $\mathbf Z/rs\mathbf Z\longrightarrow (\mathbf Z/r\mathbf Z)\times (\mathbf Z/s\mathbf Z)$ induce, per restrizione, una bigezione $\mathcal U(\mathbf Z/rs\mathbf Z)\longrightarrow \mathcal U(\mathbf Z/r\mathbf Z)\times \mathcal U (\mathbf Z/s\mathbf Z)$. Dunque, l'indicatore di Eulero $\varphi$ è moltiplicativo (i.e., per ogni $r,s\in\mathbf Z$ coprimi, si ha $\varphi(rs)=\varphi (r)\varphi(s)$). Una bigezione naturale fra un quoziente di $\mathbf R$ e $\mathbf S^1$. Caratterizzazione per l'irriducibilità di un polinomio di grado 2 o 3 in $A[T]$, dove $A\in\{\mathbf Q,\mathbf R,\mathbf C,\mathbf Z/p\mathbf Z, p\mbox{ primo}\}$. I polinomi irriducibili in $\mathbf C[T]$ sono precisamente quelli di grado 1. Se $z$ è radice complessa non reale di un polinomio $f\in\mathbf R[T]$, allora anche $\overline z$ è radice di $f$. Gli unici polinomi irriducibili di $\mathbf R[T]$ sono i polinomi di grado 1 e quelli di grado 2 che non hanno radici reali. Criterio di Eisenstein e sua versione reciproca. Esempi di fattorizzazione.
__________________________________
X Settimana (1 Dicembre - 5 Dicembre)
Criterio di irriducibilità modulo $p$ e sue applicazioni. Ricerca delle possibili radici razionali di un polinomio a coefficienti interi. Esercizi di riepilogo sulla fattorizzazione. Studio del gruppo $S(X)$ delle bigezioni (o permutazioni) di un insieme non vuoto $X$ in sé. Il supporto di una bigezione $f\in S(X)$ è l'insieme ${\rm Supp}(f):=\{x\in X:f(x)\neq x\}$. Due bigezioni $f,g\in S(X)$ disgiunte (i.e. ${\rm Supp}(f)\cap {\rm Supp}(g)= \emptyset$) commutano rispetto alla composizione. Nozione di $k$-ciclo di $S_n:=S(\{1,2,\ldots,n\})$. Ogni permutazione in $S_n$ si può esprimere, in modo unico (a meno di ordine), come composizione di cicli a due a due disgiunti. Esempi ed esercizi vari. Nozione di segno di una permutazione. Calcolo del segno delle trasposizioni.
 Esercizi per casa 4.
Esercizi per casa 4.
__________________________________
XI Settimana (8 Dicembre - 12 Dicembre)
Il segno di un $k$ ciclo in $S_n$ è $(-1)^{k+1}$. Uso del calcolo della struttura ciclica di una permutazione per determinare il suo segno. L'ordine di un elemento $g$ in un gruppo è uguale alla cardinalità del gruppo che $g$ genera. Se $g$ è un elemento di ordine $s$ allora l'ordine di $g^k$ è $\dfrac{s}{{\rm MCD}(k,s)}$. Se $G$ è un gruppo ciclico di ordine $s$, per ogni divisore $d$ di $s$ esiste un unico sottogruppo di $G$ di cardinalità $d$. Esempi di calcolo di sottogruppi di gruppi ciclici e loro generatori. Se $g,h$ sono elementi di un gruppo qualsiasi $G$ aventi ordini coprimi $r,s$, se $gh=hg$ allora l'ordine di $gh$ è $rs$. L'ordine di un $k$-ciclo in $S_n$ è $k$. Uso della struttura ciclica di una permutazione per il calcolo del suo ordine. Esempi espliciti di descrizione della partizione individuata dai laterali sinistri rispetto a un sottogruppo. Teorema di Lagrange, dimostrazione e applicazioni. Se $G$ è un gruppo con $n$ elementi, allora $g^n=1$, per ogni $g\in G$. Dal Teorema di Lagrange segue il Teorema di Eulero-Fermat. Se $p$ è un numero primo e $G$ è un gruppo con $p$ elementi, allora $G$ è ciclico. Classificazione dei gruppi ciclici: un gruppo ciclico infinito è isomorfo a $\mathbf Z$; un gruppo ciclico finito con $s$ elementi è isomorfo a $\mathbf Z/s\mathbf Z$. Classificazione dei gruppi con 4 elementi. Esempi di sottogruppi non normali.
__________________________________
XII Settimana (15 Dicembre - 19 Dicembre)
Se $G$ è un gruppo con $n$ elementi e $H$ è un sottogruppo di $G$ avente cardinalità $d$, allora entrambe le partizioni indotte dalle relazioni di equivalenza (sinistra e destra) associate a $H$ hanno $n/d$ elementi; se inoltre $n=2d$, allora $H$ è normale in $G$. Il gruppo alterno $A_n$ è normale in $S_n$. Il viceversa al Teorema di Lagrange non vale in generale: infatti $A_4$ ha 12 elementi ma non ha alcun sottogruppo di cardinalità 6. Un gruppo nel quale ogni elemento distinto da 1 ha ordine 2 è abeliano. Un gruppo di cardinalità pari ha sempre almeno un elemento di ordine 2. Calcolo degli omomorfismi di gruppi $\mathbf Z/4\mathbf Z\longrightarrow \mathbf Z/6 \mathbf Z$. Esempi notevoli di anelli e loro sottoanelli. Esempi di anelli intermedi fra $\mathbf Z$ e $\mathbf Q$: l'anello $\mathbf Z_{(2)}:=\{\frac{a}{b}:a,b\in\mathbf Z, b\mbox{ dispari}\}$. Esempi di anelli intermedi fra $\mathbf Z[T]$ e $\mathbf Q[T]$: l'anello ${\rm Int}(\mathbf Z)$ dei polinomi a valori interi. L'ampliamento di Nagata $\mathbf Z(+)\mathbf Q$ di $\mathbf Z$ su $\mathbf Q$: calcolo di divisori dello zero e invertibili. Analogie fra $\mathbf Z$ e $K[T]$, dove $K$ è un campo e $T$ è un'indeterminata su $K$. Definizione della congruenza $\equiv_f$ modulo un polinomio $f$ e anello quoziente $K[T]/(f):=K[T]/\equiv_f$. Analogie fra gli anelli $K[T]/(f)$ e $\mathbf Z/n\mathbf Z$: dato $g\in K[T]$, $[g]_f$ è invertibile in $K[T]/(f)$ se e soltanto se MCD$(f,g)=1$. L'anello $K[T]/(f)$ è un campo se e soltanto se $f$ è irriducibile in $K[T]$. Esempi di calcolo di inverso di una classe in un quoziente di anelli di polinomi. La classificazione, a meno di isomorfismi, dei gruppi di ordine 6.
 Esercizi per casa 5.
Esercizi per casa 5.
Criterio di irriducibilità modulo $p$ e sue applicazioni. Ricerca delle possibili radici razionali di un polinomio a coefficienti interi. Esercizi di riepilogo sulla fattorizzazione. Studio del gruppo $S(X)$ delle bigezioni (o permutazioni) di un insieme non vuoto $X$ in sé. Il supporto di una bigezione $f\in S(X)$ è l'insieme ${\rm Supp}(f):=\{x\in X:f(x)\neq x\}$. Due bigezioni $f,g\in S(X)$ disgiunte (i.e. ${\rm Supp}(f)\cap {\rm Supp}(g)= \emptyset$) commutano rispetto alla composizione. Nozione di $k$-ciclo di $S_n:=S(\{1,2,\ldots,n\})$. Ogni permutazione in $S_n$ si può esprimere, in modo unico (a meno di ordine), come composizione di cicli a due a due disgiunti. Esempi ed esercizi vari. Nozione di segno di una permutazione. Calcolo del segno delle trasposizioni.
 Esercizi per casa 4.
Esercizi per casa 4.__________________________________
XI Settimana (8 Dicembre - 12 Dicembre)
Il segno di un $k$ ciclo in $S_n$ è $(-1)^{k+1}$. Uso del calcolo della struttura ciclica di una permutazione per determinare il suo segno. L'ordine di un elemento $g$ in un gruppo è uguale alla cardinalità del gruppo che $g$ genera. Se $g$ è un elemento di ordine $s$ allora l'ordine di $g^k$ è $\dfrac{s}{{\rm MCD}(k,s)}$. Se $G$ è un gruppo ciclico di ordine $s$, per ogni divisore $d$ di $s$ esiste un unico sottogruppo di $G$ di cardinalità $d$. Esempi di calcolo di sottogruppi di gruppi ciclici e loro generatori. Se $g,h$ sono elementi di un gruppo qualsiasi $G$ aventi ordini coprimi $r,s$, se $gh=hg$ allora l'ordine di $gh$ è $rs$. L'ordine di un $k$-ciclo in $S_n$ è $k$. Uso della struttura ciclica di una permutazione per il calcolo del suo ordine. Esempi espliciti di descrizione della partizione individuata dai laterali sinistri rispetto a un sottogruppo. Teorema di Lagrange, dimostrazione e applicazioni. Se $G$ è un gruppo con $n$ elementi, allora $g^n=1$, per ogni $g\in G$. Dal Teorema di Lagrange segue il Teorema di Eulero-Fermat. Se $p$ è un numero primo e $G$ è un gruppo con $p$ elementi, allora $G$ è ciclico. Classificazione dei gruppi ciclici: un gruppo ciclico infinito è isomorfo a $\mathbf Z$; un gruppo ciclico finito con $s$ elementi è isomorfo a $\mathbf Z/s\mathbf Z$. Classificazione dei gruppi con 4 elementi. Esempi di sottogruppi non normali.
__________________________________
XII Settimana (15 Dicembre - 19 Dicembre)
Se $G$ è un gruppo con $n$ elementi e $H$ è un sottogruppo di $G$ avente cardinalità $d$, allora entrambe le partizioni indotte dalle relazioni di equivalenza (sinistra e destra) associate a $H$ hanno $n/d$ elementi; se inoltre $n=2d$, allora $H$ è normale in $G$. Il gruppo alterno $A_n$ è normale in $S_n$. Il viceversa al Teorema di Lagrange non vale in generale: infatti $A_4$ ha 12 elementi ma non ha alcun sottogruppo di cardinalità 6. Un gruppo nel quale ogni elemento distinto da 1 ha ordine 2 è abeliano. Un gruppo di cardinalità pari ha sempre almeno un elemento di ordine 2. Calcolo degli omomorfismi di gruppi $\mathbf Z/4\mathbf Z\longrightarrow \mathbf Z/6 \mathbf Z$. Esempi notevoli di anelli e loro sottoanelli. Esempi di anelli intermedi fra $\mathbf Z$ e $\mathbf Q$: l'anello $\mathbf Z_{(2)}:=\{\frac{a}{b}:a,b\in\mathbf Z, b\mbox{ dispari}\}$. Esempi di anelli intermedi fra $\mathbf Z[T]$ e $\mathbf Q[T]$: l'anello ${\rm Int}(\mathbf Z)$ dei polinomi a valori interi. L'ampliamento di Nagata $\mathbf Z(+)\mathbf Q$ di $\mathbf Z$ su $\mathbf Q$: calcolo di divisori dello zero e invertibili. Analogie fra $\mathbf Z$ e $K[T]$, dove $K$ è un campo e $T$ è un'indeterminata su $K$. Definizione della congruenza $\equiv_f$ modulo un polinomio $f$ e anello quoziente $K[T]/(f):=K[T]/\equiv_f$. Analogie fra gli anelli $K[T]/(f)$ e $\mathbf Z/n\mathbf Z$: dato $g\in K[T]$, $[g]_f$ è invertibile in $K[T]/(f)$ se e soltanto se MCD$(f,g)=1$. L'anello $K[T]/(f)$ è un campo se e soltanto se $f$ è irriducibile in $K[T]$. Esempi di calcolo di inverso di una classe in un quoziente di anelli di polinomi. La classificazione, a meno di isomorfismi, dei gruppi di ordine 6.
 Esercizi per casa 5.
Esercizi per casa 5.__________________________________
TUTORATO (a cura di Stefano Caporro e Sara D'Ettorre)
 10 Ottobre 2014
10 Ottobre 2014 15 Ottobre 2014
15 Ottobre 2014  24 Ottobre 2014
24 Ottobre 2014 29 Ottobre 2014
29 Ottobre 2014 31 Ottobre 2014
31 Ottobre 2014 14 Novembre 2014
14 Novembre 2014 21 Novembre 2014
21 Novembre 2014 28 Novembre 2014
28 Novembre 2014 4 Dicembre 2014
4 Dicembre 2014 12 Dicembre 2014
12 Dicembre 2014 19 Dicembre 2014
19 Dicembre 2014 9 Gennaio 2015
9 Gennaio 2015
Alcune ..... pseudo-dimostrazioni
(trovare gli errori)
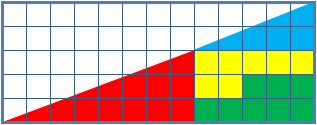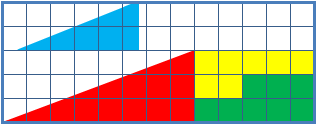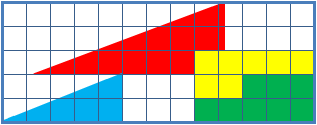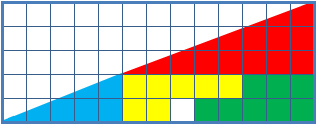
Il quadratino .... perduto

64 = 65 ??